Codeforces Problems の不具合対応

CF Problems トラブルシュート 開発

概要

Codeforces Problems で特定の問題が大量に表示される不具合が発生しました。 原因はクローラのバグだったので直しました。

はじめに

Codeforces Problems は私が開発した Codefores で出題された問題およびその各ユーザーごとの正答状況を確認しやすくするための Web アプリケーションです. AtCoder Problems を模倣して作りました。

cf.kira924age.com

最近 Codeforces Round #822 (Div. 2) が重複して大量に表示されるという不具合が発生しました。

この記事では事象の原因および解決方法について述べます。

発生する事象

以下の画像に示すように同じコンテストが重複して大量に表示されています。

大量に表示される #822 (Div. 2)

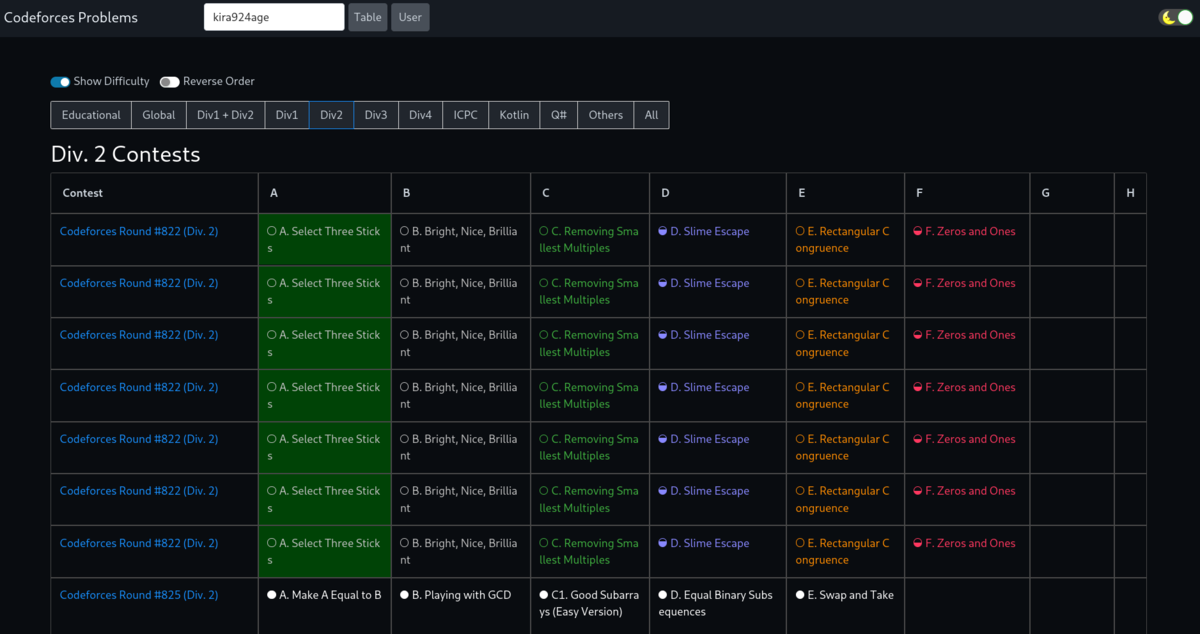
原因の究明

Codeforces Problems では1日1回クローラにより問題のデータを fetch して json ファイルに書き出しています。

コンテストおよび問題のデータが格納されている contests.json を確認したところ、#822 (Div. 2) が重複して格納されていました。

$ cat contests.json | grep 1734
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
  "id": 1734,
$ cat contests.json | grep 1734 | wc -l
25

数えてみたら25個同じコンテストの情報が格納されていました。

コンテストの情報の書き込み時の処理を見たところ以下のような Python コードで実装されていました。

source: https://github.com/kira924age/CodeforcesProblems/blob/5b2f521117e98481f6581c113ef1b6dc26c1a740/cf-problems-crawler/update_data.py#L37-L52

    if idx != -1:
        prev_contest = contest_json[idx]
        if prev_contest["problems"] is None:
            contest_json[idx] = add
        elif len(add["problems"]) > len(prev_contest["problems"]):
            contest_json = [add] + contest_json
        elif len(add["problems"]) == len(prev_contest["problems"]):
            for i, (prev_problem, add_problem) in enumerate(
                    zip(prev_contest["problems"], add["problems"])):

                if prev_problem != None and "rating" in prev_problem:
                    continue

                contest_json[idx]["problems"][i] = add_problem
    else:
        contest_json = [add] + contest_json

idx という変数は更新前のコンテスト情報が格納されているインデックスです。 バグの原因は 1つめ elif ブロックでの記述です。

        elif len(add["problems"]) > len(prev_contest["problems"]):
            contest_json = [add] + contest_json

同じコンテストの情報に関して新しいものと古いものを比較して、新しいほうが古いものより問題数が多かった場合、古い情報とは別にデータを追加しています。

これにより、#822 が無限に書き込まれていました。何を意図したコードなのかは不明です。

以下のコミットによりこのバグを修正しました。

github.com

また重複して書き込まれた情報については手で直しました。

github.com

終わりに

久しぶりにこのアプリのコードを読んだのですが、今回関連するコードだけ見てもかなりひどかったので近いうちにリファクタリングしたいと思います。

長らく放置している issues の対応もそのうちします。

今回の作業は着手してから記事の執筆も含めて1時間程度で終わったので隙間時間を使ってこれからもちょいちょい手直ししていきたいと思います。

Linux でマイクの入力音量が勝手に下がる問題

Linux PulseAudio

概要

Linux で有線接続のマイクの入力音声のボリュームが勝手に下がる現象が発生しました. これは Zoom や Google Chrome といったクライアントが勝手にデバイスの音量を操作することが原因であることが分かりました。 また Pulse Audio 側でクライアントによる音量操作を無効化するオプションは現時点では用意されていないようでした。

そこで以下のようなスクリプトを常時実行するという手法によりデバイス音量を一定に保つことでクライントによる音量操作を事実上無効化することに成功しました。 (alsa_input.???-?????.analog-stereo はデバイス名で適切に置換する必要があります)

$ while sleep 0.1; do pacmd set-source-volume alsa_input.???-?????.analog-stereo 65535; done

環境

以下のようなソフトウェアを使用している環境で検証しました.

  • OS : Ubuntu 20.04
  • デスクトップ環境 : GNOME 3.36.5
  • サウンドサーバー : pulseaudio 13.99.1
  • Zoom : Version: 5.9.3 (1911)
$ cat /etc/os-release
NAME="Ubuntu"
VERSION="20.04.3 LTS (Focal Fossa)"
ID=ubuntu
ID_LIKE=debian
PRETTY_NAME="Ubuntu 20.04.3 LTS"
VERSION_ID="20.04"
HOME_URL="https://www.ubuntu.com/"
SUPPORT_URL="https://help.ubuntu.com/"
BUG_REPORT_URL="https://bugs.launchpad.net/ubuntu/"
PRIVACY_POLICY_URL="https://www.ubuntu.com/legal/terms-and-policies/privacy-policy"
VERSION_CODENAME=focal
UBUNTU_CODENAME=focal
$ gnome-shell --version
GNOME Shell 3.36.9
$ pulseaudio --version
pulseaudio 13.99.1

事象の再現

Zoom Version: 5.9.3 (1911)

Zoom で会議に参加してマイクを有線接続。ミュートを解除して何かしらの音をマイクに拾わせたところ自動的にマイクの音量が小さくなりました。 音量の設定にはデバイスごとの設定とアプリごとの設定がありますが、今回自動的に下がったのはデバイスごとの設定のみでした。

以下のキャプチャは GNOME のデフォルトのシステム設定を行う GUI である 設定 (Setting) のサウンド設定の画面です。 入力デバイスの音量が自動的に下がっていることが確認できます。(もちろん音量を手動で下げているわけではありません)

f:id:kira000:20220216211200g:plain

Google Chrome (Google Meet)

この問題は Zoom 固有の問題ではなく他のアプリケーションでも発生しました。 Google Chrome 上で Google Meet を起動し会議に参加してマイクに音声を拾わせた場合も同様の事象が発生しました。

f:id:kira000:20220216212306g:plain

原因

ググったら同様の事象についての質問が既にありました。

lists.freedesktop.org

askubuntu.com

どうやら Zoom や Google Chrome といったクライアントアプリ側で自動で入力デバイスの音量を調節するという迷惑な機能があるようです。 Zoom の場合は以下のように Automaticcaly adjast microphone volume という設定項目があり, クライアント側でこの機能をオフにすることができました。

f:id:kira000:20220216213727p:plain

実際にこの機能をオフにした状態で Zoom で会議に参加してマイクに音を拾わせたところ自動的に音量が変化する現象はなくなりました。

しかし, Google Chrome で Google Meet のようなアプリを起動している場合はアプリ側でこの機能をオフにすることはできなさそうでした。 以下に引用するように, Google Chrome ではおそらく WebRTC プロトコルが使われており, Chrome/Chromium の WebRTC 実装には Auto Gain Control という機能があり, ウェブアプリ自体にこの機能をオフにするオプションが無い限りオフにできないらしいです。

Unfortunately the WebRTC implementation in Chromium comes with a handy “feature” called Automatic Gain Control that tends to screw with your microphone volume. Unless the web app itself gives you an option to disable it, there is otherwise no way turn it off, and Chrome developers don't want to add a global “off switch” for it.

また, PulseAudio 側でクライアントによる音量操作を無効化するオプションは現時点では用意されていないようでした。issue がたっていました。

解決策

下記の質問の解答の内最も upvote が多いものを試したところクライアント側で入力デバイスの音量を変更を事実上禁止することができました。

手法は単純で以下のスクリプトを実行するだけです。

$ while sleep 0.1; do pacmd set-source-volume alsa_input.???-?????.analog-stereo 65535; done

なお, alsa_input.???-?????.analog-stereo のところは下記のコマンドで得られるデバイス名で適切に置換する必要があります。

$ pacmd list-sources | grep alsa_input
        name: <alsa_input.usb-USB_HD_Camera_USB_HD_Camera-02.iec958-stereo>
        name: <alsa_input.pci-0000_00_1b.0.analog-stereo>
        name: <alsa_input.usb-USB_HD_Camera_USB_HD_Camera-02.iec958-stereo.echo-cancel>

私の場合は alsa_input.pci-0000_00_1b.0.analog-stereo で置換しました。

このスクリプトは 0.1 秒ごとに pacmd という PulseAudio の設定を変更するコマンドを実行してデバイスの音量を固定値としています。 65535 という値は 100% に該当します。上記の質問の解答者は 90000 (135%) に設定していました。

この手法は無駄に CPU リソースを使うのであまりエレガントな解決法とは呼べなさそうです。 しかし残念ながら現時点ではクライアントからデバイスの音量の制御を抑制する方法としてはこれくらいしかなさそうです。 今後 PulseAudio に新しいオプションが追加されることを期待したいです。(お前がコミットしろ)

このスクリプトを実行すると以下のように手動でデバイス音量を調節しようとしても固定値にすぐに戻されてしまいます。 バグっぽいですがこれは意図した通りの挙動です。

f:id:kira000:20220217200154g:plain

毎回このスクリプトを手動で実行するのは面倒なので, systemd により起動時に自動で実行するようにしてみます。

上記のシェルスクリプトを適当な場所に保存して chmod +x で実行権限を付与します。 次に、以下のように ~/.local/share/systemd/user/ に systemd ファイルを作成します。 ExecStart に渡す PATH は絶対PATHで指定しました。

$ vim ~/.local/share/systemd/user/no-agc.service
$ cat ~/.local/share/systemd/user/no-agc.service
[Unit]
After=pulseaudio.service
Requires=pulseaudio.service

[Service]
ExecStart=/home/kira924age/work/configs/saber/pulse-audio/no-agc.sh

ExecReload=/bin/kill -s HUP $MAINPID
KillSignal=SIGQUIT

TimeoutStopSec=5
KillMode=process
PrivateTmp=true
Restart=always

[Install]
WantedBy=default.target

次に以下のコマンドで自動起動を有効にします。

$ systemctl --user enable no-agc.service

再起動して service が起動していれば勝ちです。

$ sudo reboot
$ systemctl --user status no-agc.service
● no-agc.service
     Loaded: loaded (/home/kira924age/.local/share/systemd/user/no-agc.service;>
     Active: active (running) since Thu 2022-02-17 22:06:44 JST; 13s ago
   Main PID: 2141 (no-agc.sh)
     CGroup: /user.slice/user-1000.slice/user@1000.service/no-agc.service
             ├─2141 /bin/bash /home/kira924age/work/configs/saber/pulse-audio/n>
             └─4359 sleep 0.1

 2月 17 22:06:44 saber systemd[2083]: Started no-agc.service.
 2月 17 22:06:46 saber no-agc.sh[2190]: デーモンが応答しません

試したけどうまく行かなかった手法

ArchWiki の以下の項目に書いてあることも試しましたがうまく動作しませんでした。

wiki.archlinux.jp

  • /usr/share/pulseaudio/alsa-mixer/paths/analog-input*.conf に該当するファイルを検索. (Ubuntu の場合は Arch とは該当ファイルがあるディレクトリが異なっていました)
$ sudo ls /usr/share/pulseaudio/alsa-mixer/paths/ | grep -oE ^analog-input.*\.conf$
analog-input-aux.conf
analog-input-dock-mic.conf
analog-input-fm.conf
analog-input-front-mic.conf
analog-input-headphone-mic.conf
analog-input-headset-mic.conf
analog-input-internal-mic-always.conf
analog-input-internal-mic.conf
analog-input-linein.conf
analog-input-mic-line.conf
analog-input-mic.conf
analog-input-rear-mic.conf
analog-input-tvtuner.conf
analog-input-video.conf
analog-input.conf

検索に該当した全てのファイルについて以下のようにファイルを編集 (!!! PulseAudio の設定ファイルを編集する前にバックアップを取ることをおすすめします。何かあったときにすぐ元に戻せるようにしたほう良さそうです !!!)

  • [Element Capture] の下の volume を zero に設定
  • [Element Internal Mic Boost] の下の volume を zero に設定
  • [Element Int Mic Boost] の下の volume を zero に設定
  • [Element Mic Boost] の下の volume を zero に設定

(注意) [Element Headphone Mic Boost] や [Element Mic Boost (+20dB)] といった全てのバリエーションでも同様に設定する

PulseAudio を再起動して設定を反映させる。

$ pulseaudio -k
$ pulseaudio --start

この手法は PulseAudio の Auto Gain Cntorol を無効化する方法としていろいろなところで紹介されているものですが私の場合はうまく動作しませんでした。 音量が小さくなる現象はなくなりましたが、逆に大きくなる現象が発生しました。 また, /usr/share/pulseaudio/alsa-mixer/paths/ は PulseAudio のパッケージを更新するたびに上書きされるので, そのたびに編集する必要があります。

参考文献

AtCoder Problems のパクリアプリ CF Problems を作りました

競プロ 開発 Webフロントエンド CF Problems

概要

AtCoder Problems を模倣して CF Problems という Web Application を作りました.

(2021-07-07追記) 衝突を避けるためにサイト名を Codeforces Problems に改名しました.

はじめに

AtCoder Problems の Codeforces 版みたいな Web Application があったら良いなと思っていたのですが, これまでのところ私の観測する範囲では存在していませんでした.

(2021-07-07追記) あとでちゃんと探したらありました.

そして, ちょうど Web フロントエンドの勉強をしたいということもあり良い機会だと思って作りました. 下記に示すリンクから作ったものを見ることが出来ます.

cf.kira924age.com

Codeforces は Codeforces API という API を公開しているので今回はこれを利用しました. 開発の際は AtCoder Problems と yukicoder problems のコードを参考にさせてもらいました. 宇宙ツイッタラーX (@kenkoooo) さん, iiljj さん, その他のコントリビューターの皆さんに感謝してます.

CF Problems とは?

CF Problems は Codeforces API を利用して Codeforces の問題およびユーザー情報を本家とは違う形で表示するフロントエンドツールです. AtCoder Problems っぽいものを目指して作りましたが, 実装が面倒あるいは Codeforces API のみでは不可能だった機能を省きました.

まず. ページが Table と User の2種類しかありません. List は面倒だったので省きました. (今後やる気があれば実装するかもしれません)

それぞれのページの外観は以下の画像が示す通りです.

  • Table ページの外観

f:id:kira000:20210305205027p:plain
Table ページの外観

  • User ページの外観

f:id:kira000:20210305205206p:plain
User ページの外観

AtCoder Problems に寄せた外観であることが確認できます.

既知の問題点

CF Problems には現時点で把握しているだけでも以下のような問題点があります.

  • 本来表示されて欲しい問題が Table ページに表示されないことがある.

例えば直近では Codeforces Round #700 (Div. 2) のC問題以降が Table で表示されていません. これは Codeforces API の仕様なのでフロントエンド側で対処するのは難しそうです. なので当分あるいは永遠に改善されないと思います.

(2021-07-07追記) GitHub Actions でクローラを定期実行することでこの問題は解決しました.

issue URL : Div1 と Div2 の併設回で共通で出題されている問題がテーブルページにおいてどちらか一方にしか表示されない · Issue #1 · kira924age/CodeforcesProblems · GitHub

  • Dark Theme で Table を Chrome 系のブラウザで表示すると右に謎の白い線が入る

以下の画像に示すとおり謎の白い線が Table に右側に表示されています. CSS を色々いじったのですが消えてくれないです. ちなみに FireFox ではなぜか表示されません. 意味不明です.

f:id:kira000:20210305213750p:plain
謎の白い線

(2021-09-12追記) 何もしてないのに今見たら手元の環境では治ってました. ブラウザ (Chrome) のバグだったのかも?

  • コードが雑

これは機能的な問題ではないのですが, コードがとても雑です. Web フロントエンド初心者が雑に書いたものなのでそれはそうです. 具体的に言うと, TypeScript の型定義をサボって any を多用した, エラーハンドリングをサボった, などがあります.

コードが雑なので把握していないバグが潜んでいる可能性は非常に高いです.

汚いコードは下記の GitHub のリポジトリから見ることが出来ます.

github.com

使用したツール

最後にアプリケーションを作る上で利用したツールを書いておきます.

GNOMEで時刻表示形式を変更する

Linux GNOME

概要

GNOMEはUnixライクなOSで動作するオープンソースのデスクトップ環境です. 現在, Ubuntu や CentOS などの多くのLinuxディストリビューションで標準のデスクトップ環境として採用されています.

今回はGNOMEにおいて時刻表示形式をどのように変更するかを調べました.

環境

以下のような環境で検証しました.

$ cat /etc/os-release 
NAME="Ubuntu"
VERSION="18.04.4 LTS (Bionic Beaver)"
ID=ubuntu
ID_LIKE=debian
PRETTY_NAME="Ubuntu 18.04.4 LTS"
VERSION_ID="18.04"
HOME_URL="https://www.ubuntu.com/"
SUPPORT_URL="https://help.ubuntu.com/"
BUG_REPORT_URL="https://bugs.launchpad.net/ubuntu/"
PRIVACY_POLICY_URL="https://www.ubuntu.com/legal/terms-and-policies/privacy-policy"
VERSION_CODENAME=bionic
UBUNTU_CODENAME=bionic
$ gnome-shell --version
GNOME Shell 3.28.4

設定 (Settings)

設定 (Settings) からは表示形式を 24時制/12時制 のいずれかに変更することができます.

この変更画面にたどり着くのも少し面倒なので手順を述べます.

  • 設定 (Settings) を開く. (左上の アクティビティ (Activity) ボタンを押して, Settings と入力すると開けます)
  • サイドバーの一番下の詳細 (Details) ボタンを押す.
  • サイドバーの日付と時刻 (Date & Time) を押す.

Tweaks

GNOMEのUIのカスタマイズをGUIから行える Tweaks というツールがあります.

下記のコマンドでインストールできます.

$ sudo apt install gnome-tweaks

Tweaks のトップバー (topbar) という項目から日付や秒を表示するかどうかを選択できます.

Clock Override

Clock Override というGNOMEの拡張機能により, ステータスバー(トップバー)の時刻表示形式を変更することができます.

インストールはブラウザ経由で行う方法とUbuntuソフトウェアセンターから方法があります.

Ubuntu ソフトウェアセンターまたは https://extensions.gnome.org の検索バーに Clock Override と入力して適当にボタンを押せばインストールできます.

拡張機能は Tweaks の拡張機能/Extension という項目から設定できます.

Clock Override を使うことで, トップバーに表示される時計の時刻表示形式は自由に変更できます.

Datetime Format

Datetime Format というGNOMEの拡張機能により, トップバーおよび日付メニューの時刻表示形式を変更することができます.

文字コードに日本語を含むものを指定すると, 設定自体はできるのですが, それ以降この拡張機能の設定をしようとすると以下のようなエラーが出ます.

Error: Failed to convert locale string to UTF8: 変換する入力に無効なバイトの並びがあります

Stack trace:
  dateTimeFormat@/home/kira/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com/Utilities.js:15:20
  create/updatePreview@/home/kira/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com/FormatTarget.js:49:25
  create@/home/kira/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com/FormatTarget.js:55:2
  buildPrefsWidget/<@/home/kira/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com/prefs.js:136:61
  buildPrefsWidget@/home/kira/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com/prefs.js:136:2
  _selectExtension@resource:///org/gnome/shell/extensionPrefs/main.js:91:22
  wrapper@resource:///org/gnome/gjs/modules/_legacy.js:82:22
  _onCommandLine@resource:///org/gnome/shell/extensionPrefs/main.js:243:17
  wrapper@resource:///org/gnome/gjs/modules/_legacy.js:82:22
  main@resource:///org/gnome/shell/extensionPrefs/main.js:397:5
  @<main>:1:43

どうやら Unicode をサポートしていないようです. Github に issue が立ってました.

GSettings

GUIによる Datetime Format の設定ができなくなったので, GSettings を使って Datetime Format の値の設定をしてみます.

GNOMEにおいて日付の表示形式を含むユーザの設定情報は dconf という設定システムにより管理されています.

GSettings は dconf のフロントツールで, 設定を行うためのAPI群です.

gsettings コマンドにより, ユーザ設定の編集を行うことができます. man gsettigns と言うコマンドを叩くとマニュアルが表示されます.

以下のコマンドで Datetime Format の key をリスト表示させてみます.

$ gsettings --schemadir ~/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com list-keys org.gnome.shell.extensions.datetime-format
datemenuday-format
statusbar-format
statusbar-toggle
datemenudate-toggle
datemenudate-format
datemenuday-toggle

statusbar-format の値を変更することでステータスバー (トップバー) の時刻表示形式を変えてみます. 日付の書式文字列は man date とするとマニュアルを参照できます.

以下のコマンドで, statusbar-format の値を %m月%d日(%a) %H:%M に変更できます.

$ gsettings --schemadir ~/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com set org.gnome.shell.extensions.datetime-format statusbar-format "%m月%d日(%a) %H:%M"

以下のコマンドで, datemenuday-format の値を %H:%M:%S に変更できます.

$ gsettings --schemadir ~/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com set org.gnome.shell.extensions.datetime-format datemenuday-format "%H:%M:%S"

以下のコマンドで, datemenudate-format の値を %Y年%m月%d日(%a) に変更できます.

$ gsettings --schemadir ~/.local/share/gnome-shell/extensions/datetime-format@Daniel-Khodabakhsh.github.com set org.gnome.shell.extensions.datetime-format datemenudate-format "%Y年%m月%d日(%a)"

これらの設定により時刻表示部分は以下のような外観となりました. カレンダーの月の値の表示の下部が少し隠れているのが気になりますが概ね良さそうです.

f:id:kira000:20200629073956p:plain

参考文献

転倒数 アルゴリズム

競プロ algorithm

転倒数 (inversion number) とは?

数列 a = {a_0, a_1, a_2 ... a_n-1 } が与えられたとき,

i < j かつ a_i > a_j を満たす (i, j) の組の個数を転倒数または反転数という.

たとえば a = {3, 1, 5, 4, 2} のとき,

i < j かつ a_i > a_j となっている組は,

(3, 1), (3, 2), (5, 4), (5, 2), (4, 2) の 5組であるから転倒数は 5 となる. (添字ではなく要素の組を列挙した)

転倒数は下記のようなバブルソートを行った際の交換回数と等しくなることが知られている. 一回の交換で反転数は1減少し, ソートが完了すると反転数は0となるのでそれはそう.

#!/usr/bin/env python3

def bubble_sort(A):
    cnt = 0
    for i in range(len(A)):
        for j in range(len(A)-1, i, -1):
            if A[j] < A[j-1]:
                A[j], A[j-1] = A[j-1], A[j]
                cnt += 1
    return cnt

直感的には転倒数は昇順ソートされた状態を正しい並びとしたとき, 正しくない並びとなっている組の数と考えることができる.

転倒数を愚直な実装で求めると時間計算量は O(n^{2}) となるが以下に示すように O(n \log{n}) のアルゴリズムが存在する.

Fenwick Tree(Binary Indexed Tree)を用いる方法

i < j かつ a_i > a_j を満たす要素を数えるには以下の 2 つの方法が考えられる.

  • i についてループを回し i < j かつ a_i > a_j となるものを数える.

  • j についてループを回し i < j かつ a_i > a_j となるものを数える.

どちらもほぼ同じように見えるが, 後者のように考えないとうまくいかない.

後者の方法で i < j かつ a_i > a_j となるものを数えるとき Fenwick Tree を使うと各 j について O(\log{n}) で求めることができる.

Fenwick Tree は区間の和の計算, 要素の値の更新がそれぞれ O(\log{n}) でできるデータ構造.

  • C++ による Fenwick Tree の実装例
struct fenwick_tree {
    typedef int T;
    T n;
    vector<T> bit;

    // 各要素の初期値は 0
    fenwick_tree(T num) : bit(num+1, 0) { n = num; }

    // a_i += w
    void add(T i, T w) {
        for (T x = i; x <= n; x += x & -x) {
            bit[x] += w;
        }
    }
    // [1, i] の和を計算.
    T sum(T i) {
        T ret = 0;
        for (T x = i; x > 0; x -= x & -x) {
            ret += bit[x];
        }
        return ret;
    }
    // [left+1, right] の和を計算.
    T sum(T left, T right) {
        return sum(right) - sum(left);
    }
};

  • 使い方

    • fenwinck_tree f_tree(n); で size n の tree を作成.
    • f_tree.sum(x) で区間 [1, x] の和を求める.

    • f_tree.sum(l, r) で区間 [l+1, r] の和を求める.

    • f_tree.add(i, w) で 0-based-index で i 番目の要素に w を足す.

Fenwick Tree は最初 a = {a_0, a_1, a_2 ... a_n-1} の数列があり, 各要素の初期値は 0 となっている.

j = 0 から n-1 までループを回し. 以下のような処理をすることで転倒数を求めることができる.

fenwinck_tree f_tree(n);

for (int j = 0; j < n; j++) {
    ans += j - f_tree.sum(a[j]);
    f_tree.add(a[j], 1);
}

fenwick tree の i 番目の値が x であるとき, 値が i である要素が x 個あるものとみなす. すると sum(a[j]) が返す値は i < j かつ a_i <= a_j の個数となる. なぜなら sum(a[j]); が実行されるとき fenwick tree に追加されている数列の要素は必ず, 現在の j より小さいときに追加されたものであり(i < j を満たす), sum(a[j]) は区間[1, a[j]] の和であるから.

数えたいのは i < j かつ a_i > a_j であるから, 現在見ている数列の要素の個数である j から sum(a[j]) を減算した値を足せば良い.

注意点としては size n の tree を作成する際の n の値は数列の最大値より大きなものを設定する必要があるという点と, 数列の要素に0以下のものがあると要素の追加ができないので下駄を履かせる必要があるという点である.

分割統治法を使う方法

以下のようなコードでマージソートを行いながら転倒数を求めることもできる. (引数として渡した配列はソートされてしまう破壊的な関数である点に注意!!!)

long long merge_cnt(vector<long long> &a) {
  int n = a.size();

  if (n <= 1) {
    return 0;
  }

  long long cnt = 0;

  vector<long long> b(a.begin(), a.begin() + n / 2);
  vector<long long> c(a.begin() + n / 2, a.end());

  cnt += merge_cnt(b);
  cnt += merge_cnt(c);

  int ai = 0, bi = 0, ci = 0;
  // merge の処理
  while (ai < n) {
    if (bi < (int)b.size() && (ci == (int)c.size() || b[bi] <= c[ci])) {
      a[ai++] = b[bi++];
    } else {
      cnt += n / 2 - bi;
      a[ai++] = c[ci++];
    }
  }
  return cnt;
}

与えられた数列を A とし, その数列を B と C に分割(Devide)する.

B, C をそれぞれソート済みとすると, Aの転倒数はBの転倒数とCの転倒数を足し, さらにBとCとの間にまたがって存在する i < j かつ a[i] > a[j] となるような組の数を足したものとなる.

数列 a = {3, 1, 5, 4, 2,} を例として考える. merge_cnt() が実行されると, 数列は以下のように再帰的に分割される.

f:id:kira000:20190223045138p:plain

A = {4, 2}, B = {4}, C = {2} とする. B と C はそれぞれサイズが1なので転倒数は0である.

BとCを merge するとき, cnt がどのように更新されるかを見る.

    while (ai < n) {
        if ( bi < b.size() && (ci == c.size() || b[bi] <= c[ci]) ) {
            a[ai++] = b[bi++];
        } else {
            cnt += n / 2 - bi;
            a[ai++] = c[ci++];
        }
    }

数列 C の要素が Aに merge されるとき (i < j), cnt は更新されている. これは転倒数の定義 (i < j and a[j] < a[i] となる i, j の組の数) を考えれば当然である.

cnt += n/2 - bi; の n/2 は数列B のサイズを表している. bi は BのインデックスでBの要素全てがAに代入されると n/2 となる. 数列Cの要素が merge されるとき, 数列 B のうちまだ merge されていない要素の個数を cnt に足している.

merge の処理が済んだ数列はきちんとソートされる.

分割された数列の転倒数を赤で示したのが下図である.

f:id:kira000:20190223050517p:plain

使用例

AOJ: ALDS1-5 D

参考文献